Resonancia en circuitos resonantes de RF

En los capítulos anteriores, hemos mencionado la resonancia en los componentes parásitos de los elementos básicos. Ahora vamos a estudiar las causas de la resonancia y cómo aprovecharla.

Resonancia en componentes sin pérdidas

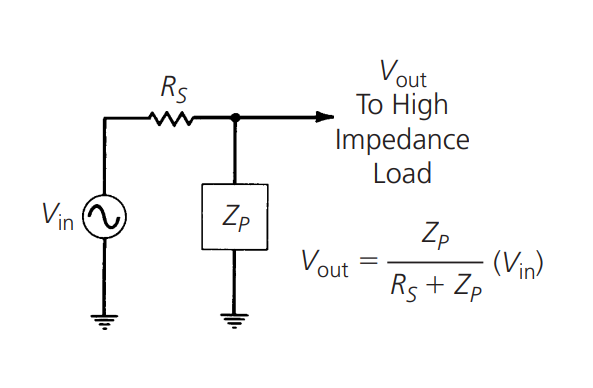
Según la regla de división de voltaje en el diagrama anterior, cuando se coloca un componente de derivación con impedancia $Z_{p}$ en la salida de un generador con resistencia interna $R_{s}$ , el voltaje de salida máximo que se puede obtener en el circuito es:

V_{o u t} = \frac{Z_{p}}{R_{s} + Z_{p}} (V_{i n})

Por lo tanto, $V_{o u t}$ siempre es menor que $V_{i n}$ . Si $Z_{p}$ es una impedancia que varía con la frecuencia (por ejemplo, una impedancia capacitiva o inductiva), entonces $V_{o u t}$ también variará con la frecuencia, y la relación entre $V_{o u t}$ y $V_{i n}$ será la ganancia del circuito (o en este caso, la pérdida), que también dependerá de la frecuencia. Por ejemplo, si usamos un condensador de 25pF como componente de derivación:

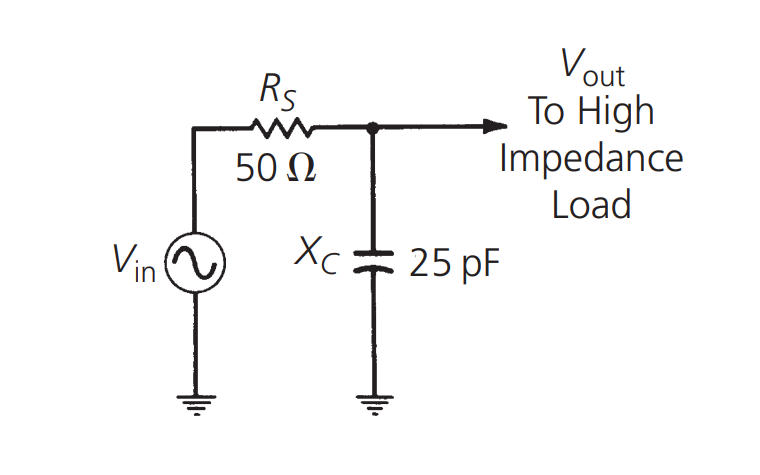
Y trazamos la función $V_{o u t} / V_{i n}$ (en dB) en función de la frecuencia:

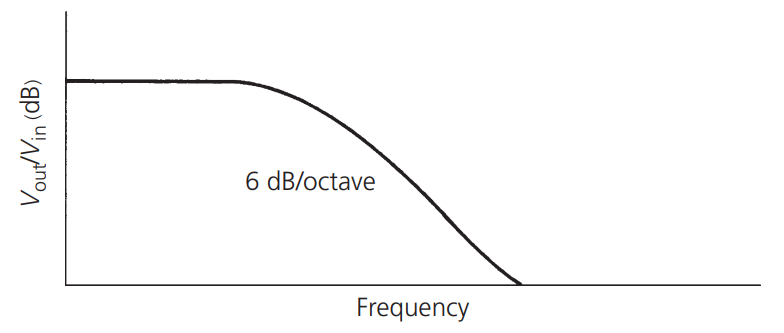
Según la siguiente fórmula:

\frac{V_{o u t}}{V_{i n}} = 20 \log_{10} \frac{X_{C}}{R_{s} + X_{C}}

Donde $\frac{V_{o u t}}{V_{i n}}$ es la pérdida expresada en dB, $R_{s}$ es la impedancia de la fuente y $X_{C}$ es la impedancia capacitiva, $X_{C} = \frac{1}{j ω C}$ .

La pérdida de este circuito RC aumentará a medida que aumente la frecuencia. Esto forma un simple filtro paso bajo. Es importante tener en cuenta que por cada duplicación de la frecuencia, la pendiente de atenuación disminuirá a una tasa de 6 dB. Esto se debe a un solo componente reactivo en el circuito. A continuación, veremos que para cada componente reactivo importante que agreguemos al circuito, la pendiente de atenuación aumentará en 6 dB adicionales.

Si reemplazamos el condensador del circuito por una bobina de 0.05µH:

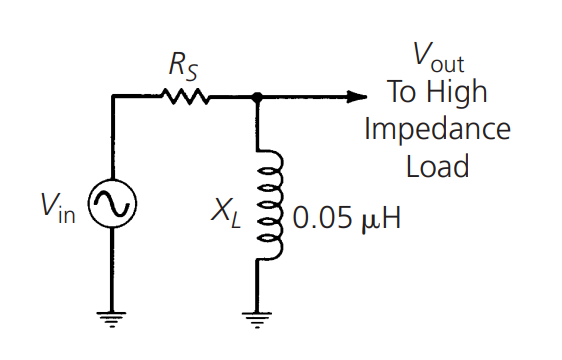
Podemos trazar la siguiente curva:

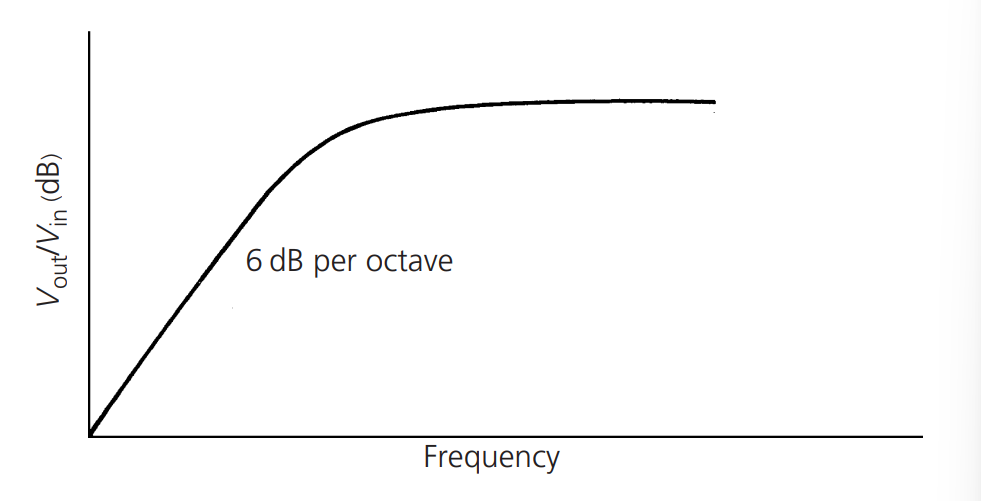
Basado en la siguiente fórmula:

\frac{V_{o u t}}{V_{i n}} = 20 \log_{10} \frac{X_{L}}{R_{s} + X_{L}}

Donde $X_{L}$ es la impedancia inductiva, $X_{L} = j ω L$ .

Esto forma un filtro paso alto simple con una pendiente de atenuación final de 6 dB/octava.

Usando la fórmula anterior, podemos trazar la respuesta en frecuencia de dos componentes reactivos independientes y opuestos. Si combinamos una bobina y un condensador en la fuente para formar un circuito LC:

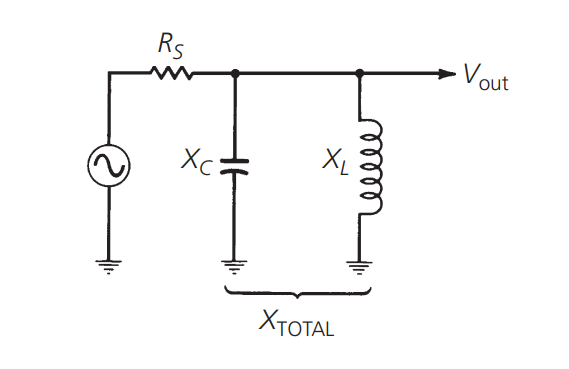
Obtendremos la siguiente curva:

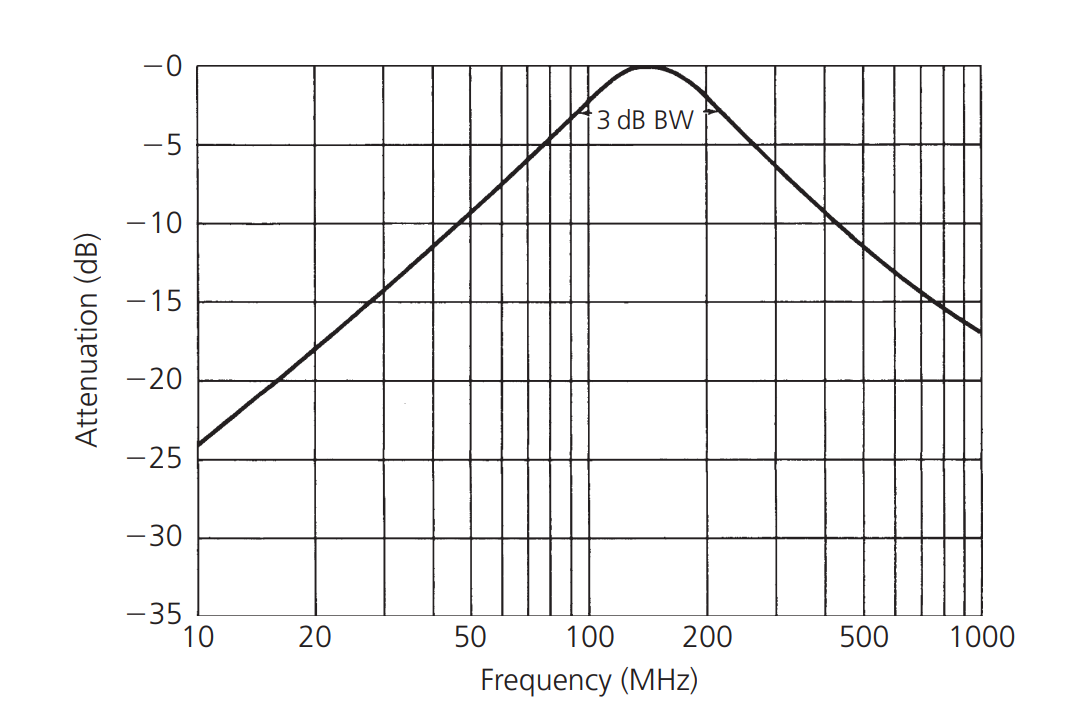
Calculado según las siguientes fórmulas:

∵ V_{o u t} = \frac{X_{t o t a l}}{R_{s} + X_{t o t a l}} (V_{i n})

∵ X_{t o t a l} = \frac{X_{C} * X_{L}}{X_{C} + X_{L}}

∵ X_{C} = \frac{1}{j ω C}

∵ X_{L} = j ω L

∴ \frac{V_{o u t}}{V_{i n}} = \frac{j ω L}{(R_{s} - ω^{2} R_{s} L C) + j ω L}

Si lo expresamos en dB, sería:

\frac{V_{o u t}}{V_{i n}} = 20 \log_{10} | \frac{j ω L}{(R_{s} - ω^{2} R_{s} L C) + j ω L} |

En la ecuación anterior, cuando nos acercamos a la frecuencia de resonancia del circuito sintonizado, la pendiente de la curva de resonancia aumenta a 12 dB/octava, esto se debe a que ambos componentes reactivos están cambiando a una velocidad de 6 dB/octava y en direcciones opuestas; sin embargo, cuando nos alejamos de la resonancia en cualquier dirección, la curva vuelve a estabilizarse con una pendiente de 6 dB/octava, ya que solo un componente reactivo está en juego, mientras que el otro presenta una impedancia muy alta en estas frecuencias y se puede ignorar en el circuito.

Los filtros RLC se pueden utilizar para seleccionar una frecuencia específica dentro del espectro total de ondas de radio ambientales, y se utilizan como filtros de paso de banda.

Referencias y Agradecimientos

"RF-Circuit-Design (segunda edición) _Chris-Bowick"

Dirección original del artículo: https://wiki-power.com/ Este artículo está protegido por la licencia CC BY-NC-SA 4.0. Si desea reproducirlo, por favor indique la fuente.

Este post está traducido usando ChatGPT, por favor feedback si hay alguna omisión.